これよく考えたら高校数学じゃなくて中学数学じゃん…
フィーリング難易度評価
<大問1>
(1)→むずかしい
(2)→かんたん
(3)→ふつう
(4)→ふつう
<大問2>
(1)→ふつう
(2)→ふつう
<大問3>
(1)→むずかしい
(2)→ふつう
<大問4>
(1)→かんたん
(2)→かんたん
(3)→ふつう
<大問5>
(1)→ふつう
(2)→ふつう
<大問6>
(1)→かんたん
(2)→ふつう
実際の入試問題は「~の値は□です」のように穴埋め形式ですが、このページでは「~の値を求めよ」のように問い方を変えているところがあります。ご了承ください。
何かありましたら下にあるコメント欄にお願いします。別解等、ありましたらぜひお願いします。
大問1
⑴
$\left(2\sqrt2-3\right)^2$を計算せよ。また、$\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}$を計算せよ。
答え(クリックで開閉)
\[\left(2\sqrt2-3\right)^2=17-12\sqrt2\] とても簡単ですが、後で役立ちます。
次、 \[\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}\] \[\small\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}\] ですけど、やった、2乗にルートがついてるから、 \[\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}\\=\sqrt{\left(10-7\sqrt2\right)-\left(7-5\sqrt2\right)}\\=\sqrt{3-2\sqrt2}\\=1-\sqrt2\] \[\small\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}\\=\sqrt{\left(10-7\sqrt2\right)-\left(7-5\sqrt2\right)}\\=\sqrt{3-2\sqrt2}\\=1-\sqrt2\] という風に、二重ルートを外せたという満足感に浸りつつ、この問題余裕だな、と思った受験生も多そうです。
ですが、天下の灘がそう甘いはずがありません。
ここで、$\sqrt{\left(3-5\right)^2}$ という式を考えてみましょう。 \[\sqrt{\left(3-5\right)^2}=\sqrt{\left(-2\right)^2}=\sqrt4=2\] \[\small\sqrt{\left(3-5\right)^2}=\sqrt{\left(-2\right)^2}=\sqrt4=2\] です。
2乗とルートを外して、$\sqrt{\left(3-5\right)^2}=3-5=-2$ ではありません。
$\sqrt{a^2}\ $は、$a>0$ のときには $+a$、$a<0$ のときには $-a$ となってしまうわけです。
これを考慮した上で、$\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}$ は、
$10>7\sqrt2$ より \[\sqrt{\left(10-7\sqrt2\right)^2}=10-7\sqrt2\] $7<5\sqrt2$ より\[\sqrt{\left(7-5\sqrt2\right)^2}=-\left(7-5\sqrt2\right)=5\sqrt2-7\]\[\small\sqrt{\left(7-5\sqrt2\right)^2}=-\left(7-5\sqrt2\right)=5\sqrt2-7\] を確認してから、
\[\sqrt{\sqrt{\left(10-7\sqrt2\right)^2}-\sqrt{\left(7-5\sqrt2\right)^2}}\\=\sqrt{10-7\sqrt2-\left(5\sqrt2-7\right)}\\=\sqrt{17-12\sqrt2}\] となります。
ここで2重ルートを外すのに少し考えるかもしれませんが、何のために先ほど$「 \left(2\sqrt2-3\right)^2=17-12\sqrt2 $」があったのか、そう、ここに出てくるからです。
\[\sqrt{17-12\sqrt2}=\sqrt{\left(2\sqrt2-3\right)^2}\] まあそれでも灘はやっぱり灘なので、喜んで2乗とルートを外して、$ \sqrt{\left(2\sqrt2-3\right)^2}=2\sqrt2-3 $とした人はさようならです。もちろんここでも、$ 2\sqrt2<3 $ を確認してから、$ \sqrt{\left(2\sqrt2-3\right)^2}=-\ \left(2\sqrt2-3\right)=3-2\sqrt2 $ $ \sqrt{\left(2\sqrt2-3\right)^2}\\=-\ \left(2\sqrt2-3\right)\\=3-2\sqrt2 $ としないといけないわけです。
よって、答えは $ 3-2\sqrt2 $ です。
コメント(クリックで開閉)
灘らしさが出ている、受験生を2段階で引っ掛ける計算問題だったと思います。
ポイントとしては言うまでもないですが、$\sqrt{a^2}$ は、$ a>0$ のときには$ +a $、$ a<0$ のときには $-a$ となります。
⑵
箱の中に、数字1が書かれたカードが1枚、数字2が書かれたカードが2枚、数字3が書かれたカードが3枚、数字4が書かれたカードが4枚、合計10枚のカードがある。この箱からAさんはカードを1枚引き、カードに描かれた数字を $a$ とする。そのカードを箱に戻さず続けてBさんはカードを1枚引き、カードに書かれた数字を $b$ とする。このとき、$a>b$ となる確率を求めよ。
答え(クリックで開閉)
① ②② ③③③ ④④④④ という風に、それぞれのカードをイメージします。そして、$a$ の数字について場合分けします。$a$ =1のときはないですから、2~4を考えます。
(ⅰ) $a$ が2のとき
$a$=2、$b$=1であり、\[\frac{2}{10}×\frac{1}{9}=\frac{2}{90}\]
(ⅱ) $a$ が3のとき
$a$=3、$b$=1or 2であり、\[\frac{3}{10}×\frac{3}{9}=\frac{9}{90}\]
(ⅲ) $a$ が4のとき
$a$ =4、$b$ =1 or 2 or 3であり、\[\frac{4}{10}×\frac{6}{9}=\frac{24}{90}\]
以上より、\[\frac{2+9+24}{90}=\frac{35}{90}=\frac{7}{18}\]
コメント(クリックで開閉)
ここでは、条件付き確率で考えていますが、条件付き確率で考えて最後に足し合わせる問題です。Aの確率の分母は10、Bの確率の分母は9で、3パターンすべて、分母はかけて90になるわけです。どうせ最後に足すときに通分するんですから、$\dfrac{3}{10}×\dfrac{3}{9}=\dfrac{1}{10}$ みたいに、一々約分する必要はないわけです。条件付き確率ではしょっちゅう出てきます。
…別に条件付き確率なんて使わなくても場合の数で35通りって出してそれを全部の90通りで割ればいいとかということを言ってしまえば終わりなんですけど。まあ、一応。
⑶
$a,\ b$ を0でない定数、$c,\ p,\ q$ を定数とする。 $x$ の方程式 $ax^2+cx+b=0$ の解が $x=5,\ p$ であり、$x$ の方程式 $bx^2+cx+a=0$の解が $x=3,\ q$ であるとき, $p+q$ の値を求めよ。
答え(クリックで開閉)
$ax^2+cx+b=0$ の解が $x=5,\ p$ で、解と係数の関係より、 \[5+p=-\frac{c}{a}\ \ \ \ldots①\] \[5p=\frac{b}{a}\ \ \ \ldots②\] $bx^2+cx+a=0$ の解が $x=3,\ q$ で、解と係数の関係より、 \[3+q=-\frac{c}{b}\ \ \ \ldots③\] \[3q=\frac{a}{b}\ \ \ \ldots④\] 未知数5つなのに式が4本しかないので不安ですが、これ以上式が立たないので仕方ないと思って進めましょう。
②の $5p=\dfrac{b}{a}$ より $b=5ap$ …⑤
⑤を④に代入して
\[3q=\frac{a}{5ap}=\frac{1}{5p}\] 運がいいことに a が消えてくれました。 $a≠0$ が条件にあるからできることです。 \[q=\frac{1}{15p}\ \ \ \ldots⑥\] ⑤と⑥を、③に代入して \[3+\frac{1}{15p}=-\frac{c}{5ap}\] 両辺に $5p$ をかけて \[15p+\frac{1}{3}=-\frac{c}{a}\ \ \ldots⑦\] ①=⑦より($-\dfrac{c}{a}$が共通のかたまり) \[5+p=15p+\frac{1}{3}\] 解いて $p=13$
これを⑥に代入して \[q=\frac{1}{15\times\dfrac{1}{3}}=\frac{1}{5}\] 以上より、 \[p+q=\frac{1}{3}+\frac{1}{5}=\frac{8}{15}\]
コメント(クリックで開閉)
地道にやっていくしかないです。でも、 $p$ や $q$ を求めるのではなく$p+q$ を求めるので、別のやり方がありそうな気がします。
あと、解と係数の関係は普段全然使わないので、よく忘れます。僕も忘れます。でも、簡単に導けるので、導き方を知っておけば忘れても安心です。
⑷
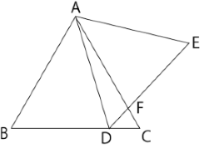
図で、△ABCと△ADEは正三角形である。
点Dは辺BC上にあり、BD>CDである。点Fは辺ACと辺DEの交点である。△ADEの面積が△ABCの面積の $\dfrac{5}{6}$ 倍であるとき、△FDCの面積は△AFEの面積の何倍か。
答え(クリックで開閉)
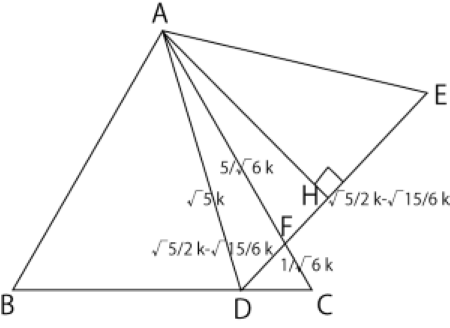
△ADEと△ABCの面積比が5:6で、2つの三角形は正三角形より相似だから、相似比は面積比の平方根で、△ADEと△ABCの相似比は$\sqrt5:\sqrt6$ となるわけです。
よって、AD:AC=$\sqrt5:\sqrt6$
また、△ADCと△AFDは相似(証明は簡単です)より、
AF:AD=AD:AC=$\sqrt5:\sqrt6$AF:AD\\=AD:AC\\=$\sqrt5:\sqrt6$ $AD=\sqrt5\ k$ とおいてやると、 \[AC=\sqrt6\ k\] \[AF=\frac{\sqrt5}{\sqrt6}\times\sqrt5\ k\ \\=\frac{5}{\sqrt6}\ k\] そして、\[FC=AC-AF=\sqrt6\ k-\frac{5}{\sqrt6}k=\frac{1}{\sqrt6}k\]\[FC\\=AC-AF\\=\sqrt6\ k-\frac{5}{\sqrt6}k\\=\frac{1}{\sqrt6}k\] \[AF:FC=\frac{5}{\sqrt6}k:\frac{1}{\sqrt6}k=5∶1 …①\] \[AF:FC\\=\frac{5}{\sqrt6}k:\frac{1}{\sqrt6}k=5∶1 …①\] ここで、AからDEに垂線を下ろして、その足をHとすると、△AFHで三平方の定理より、 \[\left(\frac{5}{\sqrt6}k\right)^2=\left(\frac{\sqrt{15}}{2}k\right)^2+{\rm FH}^2\] \[FH=\frac{\sqrt{15}}{6}k\] よって、\[DF\\=DH-FH\\=\frac{\sqrt5}{2}k-\frac{\sqrt{15}}{6}k\]\[EF\\=EH+FH\\=\frac{\sqrt5}{2}k+\frac{\sqrt{15}}{6}k \] ゆえに \[DF:EF\\=\left(\frac{\sqrt5}{2}-\frac{\sqrt{15}}{6}\right):\left(\frac{\sqrt5}{2}+\frac{\sqrt{15}}{6}\right) …②\] \[DF:EF\\=\small\left(\frac{\sqrt5}{2}-\frac{\sqrt{15}}{6}\right):\left(\frac{\sqrt5}{2}+\frac{\sqrt{15}}{6}\right) …②\] ①、②より、 \[△FDC\\=△AFE\times\frac{FC}{AF}\times\frac{DF}{EF}\\=△AFE\times\frac{1}{5}\times\frac{\dfrac{\sqrt5}{2}-\dfrac{\sqrt{15}}{6}}{\dfrac{\sqrt5}{2}+\dfrac{\sqrt{15}}{6}}\\=△AFE\times\frac{2-\sqrt3}{5}\]
コメント(クリックで開閉)
最後、計算めんどいですが、どうにかなるレベルです。他に簡単な方法ありませんかね。この問題に関して、当然ですが面積比と相似比は2乗 / ルートの関係になっていることを意識しないとだめです。というのも、僕は最初何も考えずにAC:AD=6:5…として無事さようなら。直角三角形で斜辺が対辺より短くなるという怪現象が発生しました。
大問2
(1) $ a,\ b,\ c$ はいずれも1以上5以下の整数である。$a,\ b,\ c$ を3辺の長さとする、正三角形でない二等辺三角形がかけるような、$a,\ b,\ c$ の組は全部で何組あるか。
(2) 1の目がかかれた面が2つ、2, 3, 4, 5の目がかかれた面が1つずつあるサイコロがある。このサイコロを3回振り、出た目を順に$x,\ y,\ z$ とする。$x,\ y,\ z$ を3辺の長さとする、正三角形でない二等辺三角形がかける確率を求めよ。
答え(クリックで開閉)
(1) まずは、$a=b$ であるとします。三角形の成立条件より、$a+b>c$ で、$a=b$ より $2a>c$
これが成り立つような組み合わせについて、$a$ の値を基準に考えます。なお、$0<c<6$は前提です。
$a=1$ → $2>c>0$ で $a≠c$ をみたす $c$ はないです。
$a=2$ → $4>c>0$ で $a≠c$ をみたす $c$ は、1, 3の2個
$a=3$ → $6>c>0$ で $a≠c$ をみたす $c$ は、1, 2, 4, 5の4個
$a=4$ →同様に4個
$a=5$ →同様に4個
よって、2+4+4+4=14個。
これは $a=b$ の条件の下なので、他に $b=c$ と $c=a$ も同様に14通りですから、
14×3=42通り
(2)
(1)と同様にして、$x=y$ として、$2x>z$ です。先ほどと同様にやっていきます。
$x=y=2$
→ $4>z>0$ で $a≠c$ をみたす$c$ は、1, 3の2個。1は2面あるから、$z$ となるのは合計で3面。
\[確率は、\frac{1}{6}\times\frac{1}{6}\times\frac{3}{6}=\frac{3}{216}\] $x=y=3$
→ $6>z>0$で $a≠c$ をみたす$c$ は、1, 2, 4, 5の4個。1は2面あるから、$z$ となるのは合計で5面。
\[確率は、\frac{1}{6}\times\frac{1}{6}\times\frac{5}{6}=\frac{5}{216}\] $x=y=4$ \[同様に \ \frac{5}{216}\] $x=y=5$ \[同様に \ \frac{5}{216}\] よって、\[\frac{3+5+5+5}{216}=\frac{18}{216}=\frac{1}{12}\] これは $x=y$ の条件の下なので、(1)同様、どの2辺を選ぶかは3通りより、 \[\frac{1}{12}\times3=\frac{1}{4}\]
コメント(クリックで開閉)
範囲に気を付け、余すことなく調べるというのはいつも大切です。ビジネスでも「MECE」という考えがあるそうです。「漏れがなく、重複がないこと」です。
大問3
$a,\ b$ は等式 $ab^2+(3a+4)b+2a+6=0$ …① を満たしている。
(1) $p=2ab+3a+4$ とする。$p^2$ を $a$ のみを用いて表せ。
(2) $a,\ b\ $ はどちらも、0でない整数とする。等式①を満たす $ a,\ b $ の値を求めよ。 <解答>(クリックで開閉)
答え(クリックで開閉)
(1)
~頭が固いサイト主の解法~
まず、$p^2\ $を $a$ のみを用いて表せということは、$b$ をどうにかしてやればいいんじゃね?と僕は考えました。
そして、①の式から $b$ を抽出するのは難しそうなので、$p=2ab+3a+4$ から $b=□$ の形を作って、①に代入すれば①の式が $p$ と $a$ だけの式になるのでいけるはず、と考えたわけです。
まあ、でも $b=□$ を①に代入すると言っても、$b^2$ なんかに代入したら大惨事になりますので、ちょっと技を使います。 \[{ab}^2+\left(3a+4\right)b+2a+6=\left(ab+a+3\right)\left(b+2\right)+b\ =0\ldots②\] \[{ab}^2+\left(3a+4\right)b+2a+6\\=\left(ab+a+3\right)\left(b+2\right)+b\ =0\ldots②\] こうすればどうにか耐えられそうです。
では、実際にやってみましょう。
$p=2ab+3a+4$ より、\[b=\frac{p-3a-4}{2a}\] これを②に代入して、
\[\left(a\times\frac{p-3a-4}{2a}+a+3\right)\left(\frac{p-3a-4}{2a}+2\right)+b\ =0\] \[\left(\frac{p-a+2}{2}\right)\left(\frac{p+a-4}{2a}\right)+\frac{p-3a-4}{2a}\ =0\] \[\frac{p^2+ap-4p-ap-a^2+4a+2p+2a-8+2p-6a-8}{4a}=0\] \[p^2-a^2-16=0\] \[p^2=a^2+16\] \[\tiny\left(a\times\frac{p-3a-4}{2a}+a+3\right)\left(\frac{p-3a-4}{2a}+2\right)+b\ =0\] \[\tiny\left(\frac{p-a+2}{2}\right)\left(\frac{p+a-4}{2a}\right)+\frac{p-3a-4}{2a}\ =0\] \[\tiny\frac{p^2+ap-4p-ap-a^2+4a+2p+2a-8+2p-6a-8}{4a}=0\] \[p^2-a^2-16=0\] \[p^2=a^2+16\] どうにかなりました。
~別解~
かなりアクロバティックな解法ですが楽です。
$p=2ab+3a+4$より、 \[\begin{eqnarray*}p^2 &=& 4a^2b^2+12a^2b+16ab+9a^2+24a+16\\ &=& 4a\left\{ab^2+\left(3a+4\right)b\right\}+9a^2+24a+16\end{eqnarray*}\] \[\scriptsize\begin{eqnarray*}p^2 &=& 4a^2b^2+12a^2b+16ab+9a^2+24a+16\\ &=& 4a\left\{ab^2+\left(3a+4\right)b\right\}+9a^2+24a+16\end{eqnarray*}\] ここで、①より、${ab}^2+\left(3a+4\right)b=-2a-6$ これを代入して、
\[p^2=4a\left(-2a-6\right)+9a^2+24a+16=a^2+16\] \[\small p^2\\=4a\left(-2a-6\right)+9a^2+24a+16\\=a^2+16\] 思いつけるなら、こっちの方が簡単でカッコいいです。
(2)
~(1)の誘導に乗った解法~
$p^2=a^2+16$より、\[p^2-a^2=16\] \[\left(p+a\right)\left(p-a\right)=16\] $p=2ab+3a+4$を代入して、
\[\left(2ab+3a+4+a\right)\left(2ab+3a+4-a\right)=16\] \[\left(2ab+4a+4\right)\left(2ab+2a+4\right)=16\] \[2\left(ab+2a+2\right)\times2\left(ab+a+2\right)=16\] \[\left(ab+2a+2\right)\times\left(ab+a+2\right)=4\] \[\scriptsize\left(2ab+3a+4+a\right)\left(2ab+3a+4-a\right)=16\] \[\scriptsize\left(2ab+4a+4\right)\left(2ab+2a+4\right)=16\] \[\scriptsize2\left(ab+2a+2\right)\times2\left(ab+a+2\right)=16\] \[\scriptsize\left(ab+2a+2\right)\times\left(ab+a+2\right)=4\] ここで、$ab+a+2=A$とおくと、
\[A\left(A+a\right)=4\] $A$、$A+a$はどちらも整数で、かけて4より、$(-1,-4)$,$(-2,-2)$,$(-4,-1)$,$(1,4)$,$(2,2)$,$(4,1)$が候補ですけど、$a\neq0$より、$A≠A+a$ですので、$\left(-2,\ -2\right)$と$\left(2,\ 2\right)$が消えます。後は調べるだけです。
(ⅰ) $A=-1,\ \ A+a=-4 のとき$
\[a=-3\] $A=ab+a+2$より、 \[-1=-3b-3+2\] \[b=0\] $b\neq0$より不適。
(ⅱ) $A=-4,\ \ A+a=-1$ のとき
\[a=3\] $A=\ ab+a+2$より、
\[-4=\ 3b+3+2$\] \[b=-3\] どちらも整数で適する。
(ⅲ) $A=1,\ \ A+a=4$ のとき
\[a=3\] $A=\ ab+a+2$より、 \[1=\ 3b+3+2\] \[b=-\frac{4}{3}\] 整数ではなく不適。
(ⅳ) $A=4,\ \ A+a=1$ のとき
\[a=-3\] $A=\ ab+a+2$より、
\[4=\ -3b-3+2\] \[b=-\frac{5}{3}\] 整数ではなく不適。
以上より、$(a, b)=(3, -3)$
~別解:(1)スルー解法~
$ab^2+\left(3a+4\right)b+2a+6=0$より、
\[a(b^2+3b+2)+4b+6=0\] \[a(b+1)(b+2)+4(b+2)=2\] \[\{a(b+1)+4\}(b+2)=2\] 以下、同様に解けます。こっちの方が速いと思います。
コメント(クリックで開閉)
整数問題は、因数分解、余りによる分類、不等式で範囲を決めるというような解法があります。ここでは、幸いなことに2乗と2乗が見えるので、2乗―2乗で因数分解できるな、という考えに至ればいいかと思います。
大問4
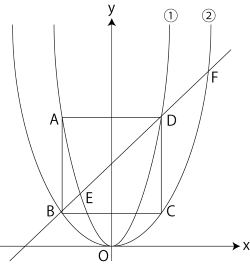
$a$ を正の定数、$t$ を2より大きい定数とする。右の図のように、$x$ 座標が $-t$ の2点A,Bと、$x$ 座標が $t$ の2点C, Dがあり、四角形 ABCDは正方形である。
関数 $y=\dfrac{1}{2}x^2$ のグラフ①は2点A, Dを通り、関数 $y={ax}^2 $のグラフ②は2点B, Cを通る。直線BDとグラフ①のD以外の交点をEとおき、直線BDとグラフ②のB以外の交点をFとおく。
(1) $a$ を $t$ を用いて表せ。
(2)点Eの $x$ 座標を $t$ を用いて表せ。
(3)原点をOとする。△OBFの面積が△OEDの面積の2倍であるとき、$t$ の値を求めよ。
答え(クリックで開閉)
(1)
$A\left(-t,\ \dfrac{1}{2}t^2\right)$で、$BC=DC=2t$ より、$B\left(-t,\ \dfrac{1}{2}t^2-2t\right)$
Bは $y={ax}^2$上の点より、代入して、
\[\frac{1}{2}t^2-2t=a\left(-t\right)^2\] $t≠0$より両辺$t$で割って、
\[\frac{1}{2}t-2=at\] \[a=\frac{1}{2}-\frac{2}{t}\] (2)
四角形ABCDが正方形より、BDの傾きは1であり、$D\left(t,\ \dfrac{1}{2}t^2\right)$だから、BDの式は、 \[y-\frac{1}{2}t^2=1\left(x-t\right)\] \[y=x-t+\frac{1}{2}t^2\] BDとグラフ①の交点がEだから、
\[y=x-t+\frac{1}{2}t^2\] \[y=\frac{1}{2}x^2\] この2つの連立方程式より、
\[x-t+\frac{1}{2}t^2=\frac{1}{2}x^2\] \[2x-2t+t^2=x^2\] \[2\left(x-t\right)=x^2-t^2\] \[2\left(x-t\right)=\left(x+t\right)\left(x-t\right)\] $x-t\neq0$より、両辺$x-t$で割って、
\[2=x+t\] \[x=2-t\] (3)
※まず、失敗例から見ていきます。
<大惨事の例>
EDの $x$ 座標の差:BFの$x$座標の差=1:2である。
Eの $x$ 座標は(2)より$2-t$、Dの$x$座標は $t$ である。
ゆえにEDの $x$ 座標の差は $t-\left(2-t\right)=2t-2$
(ここまでは良かったんですが…)
Bの $x$ 座標は $-t$ である。Fは、BDと②の交点だから、
\[y=x-t+\frac{1}{2}t^2\] \[y={\left(\frac{1}{2}-\frac{2}{t}\right)x^2}\] よって、
\[x-t+\frac{1}{2}t^2={\left(\frac{1}{2}-\frac{2}{t}\right)x^2}\] \[x-t+\frac{1}{2}t^2={\frac{1}{2}x^2-\frac{2}{t}x}^2\] \[2tx-2t^2+t^3={tx^2-4x}^2\] はい。なんということでしょう。$t^3$が出てきてしまいました。3次式なんて手に負えません。
では、どうすればよかったんでしょうか。ええ、Fの$x$座標を先に求めようとしなければいいのです。
EDの $x$ 座標の差は $2t-2$ というのがわかりましたから、BFの $x$ 座標の差は2倍の $4t-4$ です。
よって、Fの $x$ 座標は、$-t+4t-4=3t-4$となります。
DFの傾きはBDの傾きに等しく1ですから、 \[\begin{eqnarray*}1&=& \frac{a\left(3t-4\right)^2-a(-{t)}^2}{3t-4-\left(-t\right)}\\&=& \frac{a\left\{\left(3t-4\right)^2-(-{t)}^2\right\}}{3t-4-\left(-t\right)}\\&=& \frac{a\left(3t-4-t\right)\left(3t-4+t\right)}{3t-4+t}\\&=& a\left(3t-4-t\right)\\&=& a\left(2t-4\right)\end{eqnarray*}\] $a=\dfrac{1}{2}-\dfrac{2}{t}を代入して、$
\[1=\left(\frac{1}{2}-\frac{2}{t}\right)\left(2t-4\right)\] \[1=t-2-4+\frac{8}{t}\] \[t^2-7t+8=0\] 解いて、\[ t=\frac{7\pm\sqrt{17}}{2}\] $t>2$ より、\[ t=\frac{7+\sqrt{17}}{2}\]
コメント(クリックで開閉)
計算災害回避のためには、傾きというのを使うと結構回避できたりします。というのも、傾きは分子に2乗―2乗が出てきて、分母と打ち消せることがよくあるからです。
要するに、何次にもなるような連立方程式を解いて交点を求めるより、傾きから攻めていった方が楽ってことです。あと、最後の 「$t>2$」 は何気に大事です。$t>0$ みたいな「>0」の信者がいるという噂を聞いたので。
大問5

図のように、線分ABを直径とする円O上に点Cをとる。点Cを中心とし、線分ABに接する円O’をかく。さらに、円O’と線分ABの接点をDとおき、2円O、O’の交点を右の図のようにE, Fとおく。直線CDと円OのC以外の交点をGとおき、点Eが線分CHの中点となるように点Hをとる。
(1)∠CHD=∠CGEを証明せよ。
(2)2直線CG, EFの交点をMとおくと、Mは線分CDの中点であることを証明せよ。
答え(クリックで開閉)
<証明>
(1)
△CHDと△CGEにおいて、
共通より∠HCD=∠GCE …①
円の中心から弦に垂直に下ろした直線は弦を2等分するので、DG=CD …②
円O’の半径よりCD=CE …③
仮定よりCE=EH …④
②、③、④よりDG=CD=CE=EH
よって、CH=2CE=2CD=CG …⑤
①、③、⑤より、△CHD≡△CGE(2辺夾角)
したがって対応するから、∠CHD=∠CGE
<終>
(2)
<証明>
(1)より、∠CHD=∠CGE …①
弧ECに対する円周角より、∠CGE=∠CBE …②
円O’の半径よりCE=CFであるから△CEFは二等辺三角形より、∠CBE=∠CEF …③
①、②、③より、∠CHD=∠CEF
ゆえに、EFとHDは平行(同位角)。
また、CE=HEである。
したがって、中点連結定理の逆で、Mは線分CDの中点である。 <終>
コメント(クリックで開閉)
円(や球)では、「怪しい円(球)上の点と中心はつないでみる」という鉄則があります。例えばこの問題だと、僕の場合、OとO’の交点の1つであるFと、Cをつなぐことで、答えの道筋が見えてきました。 円上の点を中心と結ぶと、半径が出てくるので二等辺三角形が生まれやすいから、つなぐことが大事なのです。
大問6
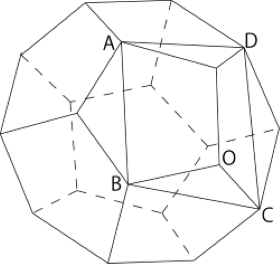
図は、一辺の長さが2の正十二面体で、O, A, B, C, Dはその頂点である。4点A, B, C, Dは同一平面上にあり、この平面をPとおく。次の問いに答えよ。なお、線分ABの長さが $1+\sqrt5$ であることは証明なしに用いてよい。
(1)点Oと平面Pの距離は1であることを証明せよ。
(2)この正十二面体を平面Pで2つの立体に切り分けたとき、点Oを含む方の立体の体積を求めよ。
答え(クリックで開閉)
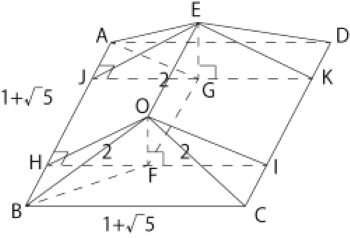
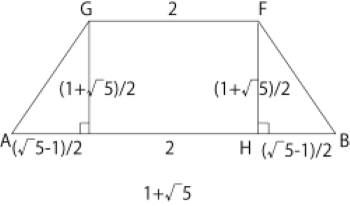
図のようになります。
<証明>
図より、△HBFで三平方の定理で、 \[FB\\=\sqrt{\left(\frac{\sqrt5+1}{2}\right)^2+\left(\frac{\sqrt5-1}{2}\right)^2}\\=\sqrt3\]
図で、△OBFにて三平方の定理より、 \[OF=\sqrt{2^2-{\sqrt3}^2}=1\] <終>
(2) \[V=四角錐O-HBCI+三角柱OHI-EJK+四角錐E-AJKD\\ =\frac{1+\sqrt5-2}{2}\times\left(1+\sqrt5\right)\times1\times\frac{1}{3}\\ \ \ \ +\left(1+\sqrt5\right)\times1\times\frac{1}{2}\times2\\ \ \ \ +\frac{1+\sqrt5-2}{2}\times\left(1+\sqrt5\right)\times1\times\frac{1}{3}\\ =\frac{2}{3}+1+\sqrt5+\frac{2}{3}\\ =\frac{7}{3}+\sqrt5\] \[Oを含む方の立体の体積\\ \ \ \ \ =四角錐O-HBCI\\ \ \ \ \ +三角柱OHI-EJK\\ \ \ \ \ +四角錐E-AJKD\\ \small={\frac{1+\sqrt5-2}{2}\times\left(1+\sqrt5\right)\times1\times\frac{1}{3}\\ \ \ \ +\small \left(1+\sqrt5\right)\times1\times\frac{1}{2}\times2\\ \ \ \ \small +\frac{1+\sqrt5-2}{2}\times\left(1+\sqrt5\right)\times1\times\frac{1}{3}}\\ =\frac{2}{3}+1+\sqrt5+\frac{2}{3}\\ =\frac{7}{3}+\sqrt5\]
コメント(クリックで開閉)
立体は高さをいかにつくるか、どんな平面で切るか、が大事です。
普通、長さがわかっていたり、辺がたくさんある方向だったりと垂直に切ることが多いです。例外ありますけど。








コメント